Presented here are the resolutions to the Yuletide mathematical enigmas posed on December 23. It is my sincere hope that you found them engaging.
Encounter 1: Imagine you are presented with nine gold coins, all appearing identical. You are informed that one coin is counterfeit and possesses less mass than the genuine ones. With a traditional beam balance scale, what is the absolute minimum number of weighings required to isolate the fraudulent coin?
Resolution: This challenge can be surmounted with merely two weighings:
(1) Segregate the nine coins into three distinct groups of three. Place two of these groups onto the balance scale. If one group is demonstrably lighter, the imposter coin resides within that trio. Should the two weighed groups achieve equilibrium, the counterfeit is located among the three unweighed coins.
(2) Now, focusing on the identified group containing the suspect coin, pit two of its members against each other on the scale. If one proves lighter, that is the fake. If they balance, the third coin in that group is the genuine counterfeit.
Encounter 2: Your temporal displacement has landed you in the past, tasked with preparing the Christmas feast. Your specific duty is to bake the festive pie. Your sole instruments are two egg timers: one calibrated for precisely four minutes, and another for precisely seven minutes. How can you achieve an exact ten-minute cooking duration?
Resolution: This puzzle admits several solutions. However, to expedite the process, consider this approach:
– Initiate both timers concurrently.
– Upon the expiration of the four-minute timer, the seven-minute timer will have exactly three minutes remaining. At this juncture, place the pie into the oven.
– When the residual three minutes on the seven-minute timer conclude, invert the seven-minute timer once more.
– Allow the seven-minute timer to complete its full cycle. Remove the pie from the oven immediately thereafter. The pie will have been subjected to precisely ten minutes of baking.
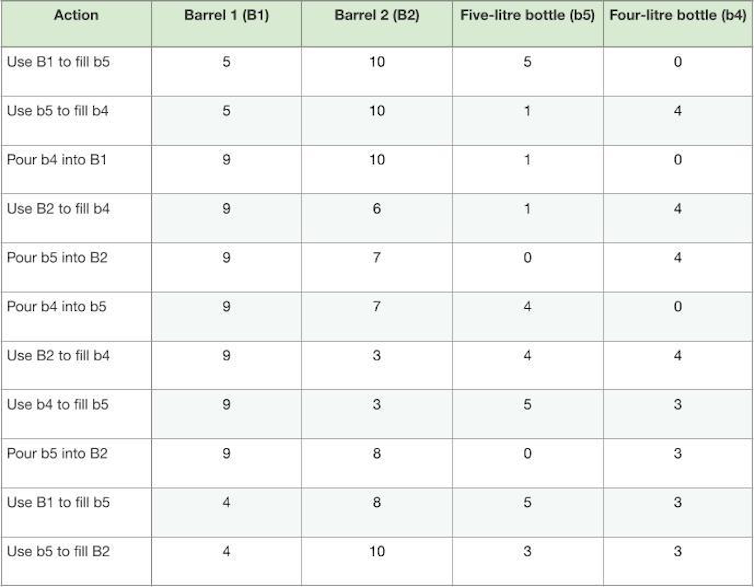
Encounter 3: Your responsibilities now extend to dispensing mulled wine, currently housed in two full ten-litre casks. The chef provides you with an empty five-litre jug and an empty four-litre jug. Your directive is to fill each jug with precisely three litres of wine, without any spillage. How can this be accomplished?
Resolution: A methodical approach involving 11 distinct steps allows for this precise measurement. The table below details the quantity of mulled wine in each cask and jug at each stage. B1 and B2 denote the initial ten-litre casks, while b5 and b4 represent the five-litre and four-litre jugs, respectively.
Please note: While a more expeditious solution may exist, this is the sequence I devised.
Encounter 4: Envision a scenario of 100 days of Christmas. On the *n*-th day, you are gifted £*n*, commencing with £1 on the inaugural day and culminating with £100 on the final day. Is it feasible to ascertain the aggregate sum bestowed upon you, bypassing a tedious summation of all 100 increments?
Resolution: When young Carl Friedrich Gauss was presented with this very query by his mathematics instructor, the precocious mathematician is reputed to have employed the following technique:
Let ‘s’ symbolize the cumulative sum of the initial 100 integers. The sum can be articulated as: s = 1 + 2 + 3 + 4 + … + 99 + 100
Alternatively, the sum can be expressed in reverse order: s = 100 + 99 + 98 + … + 4 + 3 + 2 + 1
By vertically summing these two equations term by term, the left-hand side yields s + s = 2s.
On the right-hand side, a parallel vertical summation reveals that each paired set of terms totals precisely 101 (e.g., 1 + 100, 2 + 99, and so forth). Given that there are 100 such pairs, the straightforward calculation for the total on the right-hand side is 100 * 101 = 10,100.
Consequently, 2s = 10,100, which resolves to s = 5,050. The total monetary value of your gifts amounts to £5,050.
Encounter 5: Behold a festive numerical progression. The initial six elements of this sequence are: 9, 11, 10, 12, 9, 5 … (Kindly note, the fifth element is cited as 11 in certain iterations of this puzzle.) What is the succeeding element in this array?
Resolution: This sequence delineates the quantity of letters comprising the enumeration of gifts presented over the 12 days of Christmas. Therefore, the subsequent number is 5, corresponding to “swans.” The complete roster is as follows:
Partridge (9 letters), turtle doves (11 letters), French hens (10 letters), calling birds (12 letters), gold rings (9 letters, or 11 for those inclined to the “golden” rendition), geese (5 letters), swans (5 letters), maids (5 letters), ladies (6 letters), lords (5 letters), pipers (6 letters), drummers (8 letters).
A point of consideration: While this may appear to transcend the realm of pure mathematics, the discipline of mathematics, and more broadly, critical and creative reasoning, fundamentally involves the identification of patterns, even those that initially seem somewhat obscure. The selection process for Bletchley Park, the Allies’ code-breaking headquarters during World War II, incorporated an assessment of candidates’ aptitude for solving cryptic crosswords.
Encounter 6: Among the following 100 declarations, which single statement stands as the sole verity?
- Precisely one statement within this compilation is erroneous.
- Precisely two statements within this compilation are erroneous.
- …and so forth, continuing until:
- Precisely 99 statements within this compilation are erroneous.
- Precisely 100 statements within this compilation are erroneous.
Resolution: Only the 99th statement presented possesses factual accuracy. Given that there are 100 statements in total, and the *n*-th statement posits that exactly ‘n’ statements within the list are false, this assertion can only hold true when n equals 99.
Encounter 7: You and your companions, Arthur and Bob, are adorned with Christmas hats, each being either red or green. No individual can perceive the hue of their own headwear, yet all can observe the hats worn by the other two. Arthur’s and Bob’s hats are both confirmed to be red.
You are collectively informed that at least one hat is red. Arthur then articulates: “I am unable to ascertain the color of my hat.” Subsequently, Bob declares: “I too, am unable to determine the color of my hat.” Assuming your friends possess flawless logical faculties, can you deduce the color of your own Christmas hat?
Resolution: Your hat must invariably be red. If your hat were green, then both Arthur and Bob would be observing one green hat and one red hat. In such a scenario, when Arthur states his inability to identify his hat’s color, Bob would be able to immediately deduce that his own hat must be red. However, since Bob also expresses uncertainty regarding his hat’s color, this implies Bob is observing two red hats. Therefore, you can logically conclude that your own hat is red.

Encounter 8: Beneath your Christmas tree lie three distinct boxes. One contains a pair of small presents, another houses two pieces of coal, and the third holds one small present alongside a piece of coal. Each box bears a label indicating its contents. However, these labels have been inadvertently interchanged, resulting in every box being erroneously identified.
You are permitted to retrieve a single item from one box only. Which box should you select to enable the subsequent rearrangement of labels, ensuring each label accurately reflects its box’s contents?
Resolution: Given that every box is mislabeled, you can confidently infer that if you select the box currently marked as containing “one small present and one piece of coal,” you will invariably discover either two small presents or two pieces of coal within.
Hypothetically, if you retrieve two small presents from this box, then the label designated for “two small presents” must be affixed to this particular box. Furthermore, knowing that each box was initially assigned an incorrect label, the label indicating “one small present and one piece of coal” should be transferred to the box presently marked as containing “two pieces of coal.” Finally, the label for “two pieces of coal” rightfully belongs to the box that was originally identified as containing “two small presents.”
Encounter 9: Within the kitchen, there exists a one-litre bottle of orange juice and an identical one-litre bottle of apple juice. Jack commences by transferring a tablespoon of orange juice into the apple juice bottle, thoroughly agitating it to ensure uniform distribution. Subsequently, Jill extracts a tablespoon of this now-mixed liquid from the apple juice bottle and transfers it back into the orange juice bottle. Query: Is there now a greater quantity of orange juice present in the apple juice bottle, or a greater quantity of apple juice present in the orange juice bottle?
Resolution: The quantities are precisely equal. This scenario serves as an illustrative instance of “invariance,” a concept frequently encountered in mathematical discourse.
Following all the exchanges of liquid and subsequent mixing, the volume of orange juice that has migrated into the apple juice bottle must have displaced an equivalent volume of apple juice that was originally present in that bottle. This is because the total volume of liquid within each bottle remains unchanged at one litre – the volumes themselves have remained invariant.
While this explanation might initially seem unsatisfying, the principle of invariance permits a definitive conclusion regarding the equality of quantities without recourse to numerical calculation.
Encounter 10: In the esteemed homeland of Santa Claus, all currency notes feature imagery of either Santa Claus or Mrs. Claus on one side, and either a present or a reindeer on the reverse. A junior elf arranges four notes on a surface, displaying the following in sequence:
Santa | Mrs Claus | Present | Reindeer
An elder, more experienced elf then imparts this directive: “If Santa is depicted on one side of a note, then a present must be present on the opposing side.” Which specific notes must the junior elf invert to verify the veracity of the older elf’s statement?
Resolution: Initially, the junior elf should turn over the banknote bearing Santa’s image. Should a present not be visible on the reverse, the older elf’s assertion would be invalidated. Subsequently, the junior elf should invert the banknote with the reindeer depicted. Again, if Santa were to appear on the other side, this would contradict the older elf’s pronouncement.
It might be tempting to inspect the banknote displaying a present. However, the older elf’s statement establishes a conditional relationship: “if Santa, then present.” This does not imply the converse, “if present, then Santa.” Consequently, the identity of the image on the reverse of the present banknote is inconsequential – whether it be Santa or Mrs. Claus. Similarly, the image on the reverse of the Mrs. Claus banknote is irrelevant, as the older elf’s statement offers no guidance concerning these particular notes.

Supplemental Puzzle Resolution
Santa embarks on his sleigh journey from Greenland to the North Pole at a velocity of 30 miles per hour, and immediately commences his return trip from the North Pole to Greenland at a speed of 40 miles per hour. What is the calculated average velocity for Santa’s entire round trip?
Resolution: This particular enigma may serve as an archetype of what psychologist Daniel Kahneman termed “Thinking Fast and Slow.” Our intuitive, rapid-thinking faculty might prompt the conclusion, “simply average the two figures,” leading to an estimated 35 miles per hour. While plausible, this answer is incorrect.
A more deliberate, slower-thinking process is required, necessitating tools such as algebraic manipulation and critical analysis. Let us establish the following variables:
– ‘d’ represents the geographical distance between Greenland and the North Pole.
– ‘t₁’ denotes the temporal duration of the outbound journey.
– ‘t₂’ denotes the temporal duration of the return journey.
Employing the fundamental kinematic equation, “speed equals distance divided by time,” we can formulate:
30 = d/t₁ and 40 = d/t₂
By rearranging these expressions, we deduce that t₁ = d/30 and t₂ = d/40
Since Santa traverses the same geographical expanse in both directions, his total traversed distance is 2d. The average velocity for the complete journey is then computed by dividing this total distance by the aggregate time elapsed: 2d/(t₁ + t₂)
Substituting the values derived earlier, the average velocity of Santa’s excursion is determined as 2d/(d/30 + d/40)
Performing the summation within the denominator: (d/30 + d/40) = (4d/120 + 3d/120) = 7d/120
Therefore, Santa’s average velocity = 2d / (7d/120) = 240/7 ≈ 34.3
Crucially, in this final calculation, the ‘d’ variables (representing distance) cancel out. This algebraic characteristic signifies that we can ascertain the average velocity of the journey independent of knowing either the precise distance or the exact time taken for Santa’s travels. This illustrates the potent utility of algebra: it empowers us to manipulate and utilize quantities as placeholders, even when their specific values remain unknown.
The definitive average velocity for Santa’s journey is approximately 34.3 miles per hour.![]()







